Goal
In this tutorial you will learn how to:
- Use the OpenCV function cv::filter2D in order to perform some laplacian filtering for image sharpening
- Use the OpenCV function cv::distanceTransform in order to obtain the derived representation of a binary image, where the value of each pixel is replaced by its distance to the nearest background pixel
- Use the OpenCV function cv::watershed in order to isolate objects in the image from the background
Theory
Code
This tutorial code's is shown lines below. You can also download it from here.
#include <opencv2/opencv.hpp>
#include <iostream>
int main(int, char** argv)
{
return -1;
for(
int x = 0; x < src.
rows; x++ ) {
for(
int y = 0; y < src.
cols; y++ ) {
}
}
}
imshow(
"Black Background Image", src);
1, 1, 1,
1, -8, 1,
1, 1, 1);
Mat imgResult = sharp - imgLaplacian;
imgLaplacian.convertTo(imgLaplacian,
CV_8UC3);
imshow(
"New Sharped Image", imgResult );
src = imgResult;
imshow(
"Distance Transform Image", dist);
vector<vector<Point> > contours;
for (size_t i = 0; i < contours.size(); i++)
drawContours(markers, contours, static_cast<int>(i), Scalar::all(static_cast<int>(i)+1), -1);
imshow(
"Markers", markers*10000);
vector<Vec3b> colors;
for (size_t i = 0; i < contours.size(); i++)
{
}
for (
int i = 0; i < markers.
rows; i++)
{
for (
int j = 0; j < markers.
cols; j++)
{
if (index > 0 && index <= static_cast<int>(contours.size()))
else
}
}
return 0;
}
Explanation / Result
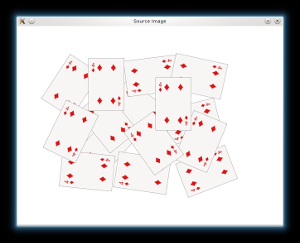
- Load the source image and check if it is loaded without any problem, then show it:
if (!src.data)
return -1;
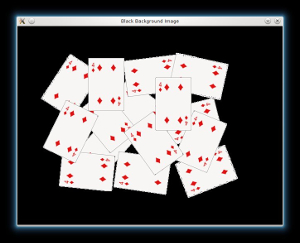
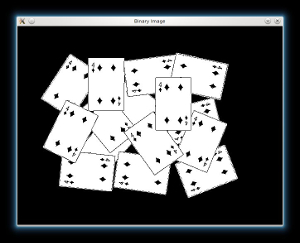
- Then if we have an image with white background, it is good to tranform it black. This will help us to desciminate the foreground objects easier when we will apply the Distance Transform:
for( int x = 0; x < src.rows; x++ ) {
for(
int y = 0; y < src.
cols; y++ ) {
if ( src.at<
Vec3b>(x, y) ==
Vec3b(255,255,255) ) {
src.at<
Vec3b>(x, y)[0] = 0;
src.at<
Vec3b>(x, y)[1] = 0;
src.at<
Vec3b>(x, y)[2] = 0;
}
}
}
imshow(
"Black Background Image", src);
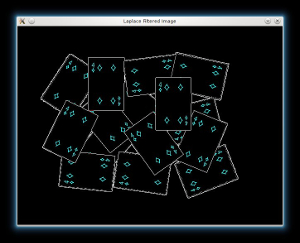
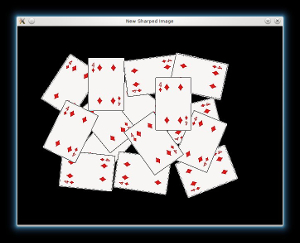
- Afterwards we will sharp our image in order to acute the edges of the foreground objects. We will apply a laplacian filter with a quite strong filter (an approximation of second derivative):
Mat kernel = (Mat_<float>(3,3) <<
1, 1, 1,
1, -8, 1,
1, 1, 1);
Mat imgLaplacian;
Mat sharp = src;
Mat imgResult = sharp - imgLaplacian;
imgLaplacian.convertTo(imgLaplacian,
CV_8UC3);
imshow(
"New Sharped Image", imgResult );
- Now we tranfrom our new sharped source image to a grayscale and a binary one, respectively:
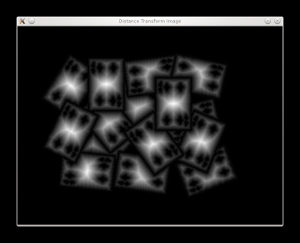
- We are ready now to apply the Distance Tranform on the binary image. Moreover, we normalize the output image in order to be able visualize and threshold the result:
Mat dist;
imshow(
"Distance Transform Image", dist);
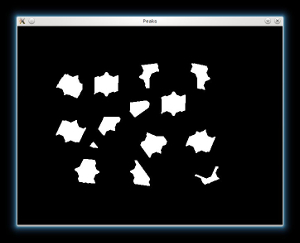
- We threshold the dist image and then perform some morphology operation (i.e. dilation) in order to extract the peaks from the above image:
Mat kernel1 = Mat::ones(3, 3,
CV_8UC1);
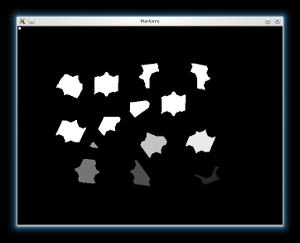
- From each blob then we create a seed/marker for the watershed algorithm with the help of the cv::findContours function:
Mat dist_8u;
vector<vector<Point> > contours;
Mat markers = Mat::zeros(dist.size(),
CV_32SC1);
for (size_t i = 0; i < contours.size(); i++)
drawContours(markers, contours, static_cast<int>(i), Scalar::all(static_cast<int>(i)+1), -1);
imshow(
"Markers", markers*10000);
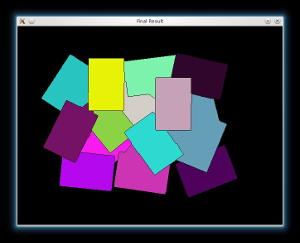
- Finally, we can apply the watershed algorithm, and visualize the result:
Mat mark = Mat::zeros(markers.size(),
CV_8UC1);
vector<Vec3b> colors;
for (size_t i = 0; i < contours.size(); i++)
{
}
Mat dst = Mat::zeros(markers.size(),
CV_8UC3);
for (int i = 0; i < markers.rows; i++)
{
for (int j = 0; j < markers.cols; j++)
{
int index = markers.at<
int>(
i,j);
if (index > 0 && index <= static_cast<int>(contours.size()))
dst.at<
Vec3b>(
i,j) = colors[index-1];
else
}
}


 1.8.11
1.8.11